Dynamics: 11.7-11.8

Watch:

https://www.khanacademy.org/science/physics/two-dimensional-motion

Example

Homework:

Simulation graph practice:
Open up the moving man simulation:
http://phet.colorado.edu/en/simulation/moving-man

Choose the "charts" tab to view x(t), v(t), and a(t) graphs.
Select "Show Vector" under velocity and acceleration
Move arrows, or type numbers into the position, velocity, and acceleration boxes - these are your starting xo, vo, and ao.
Select Record, and "Run" and watch him run!
Notice that you can pause the motion, reset x, v, and a, then continue playing.
Experiment with the play back feature. You can slow it down, and you can also grab the blue bar and move from one position of the graph to the other.
Turn on the sound to hear him crash!
Try out the Special features → Expressions evaluator.
Play around with it until you get a feel for the program, then use what you know to solve the below rectilinear motion problems!

Constant Acceleration Problems
Review + graphs

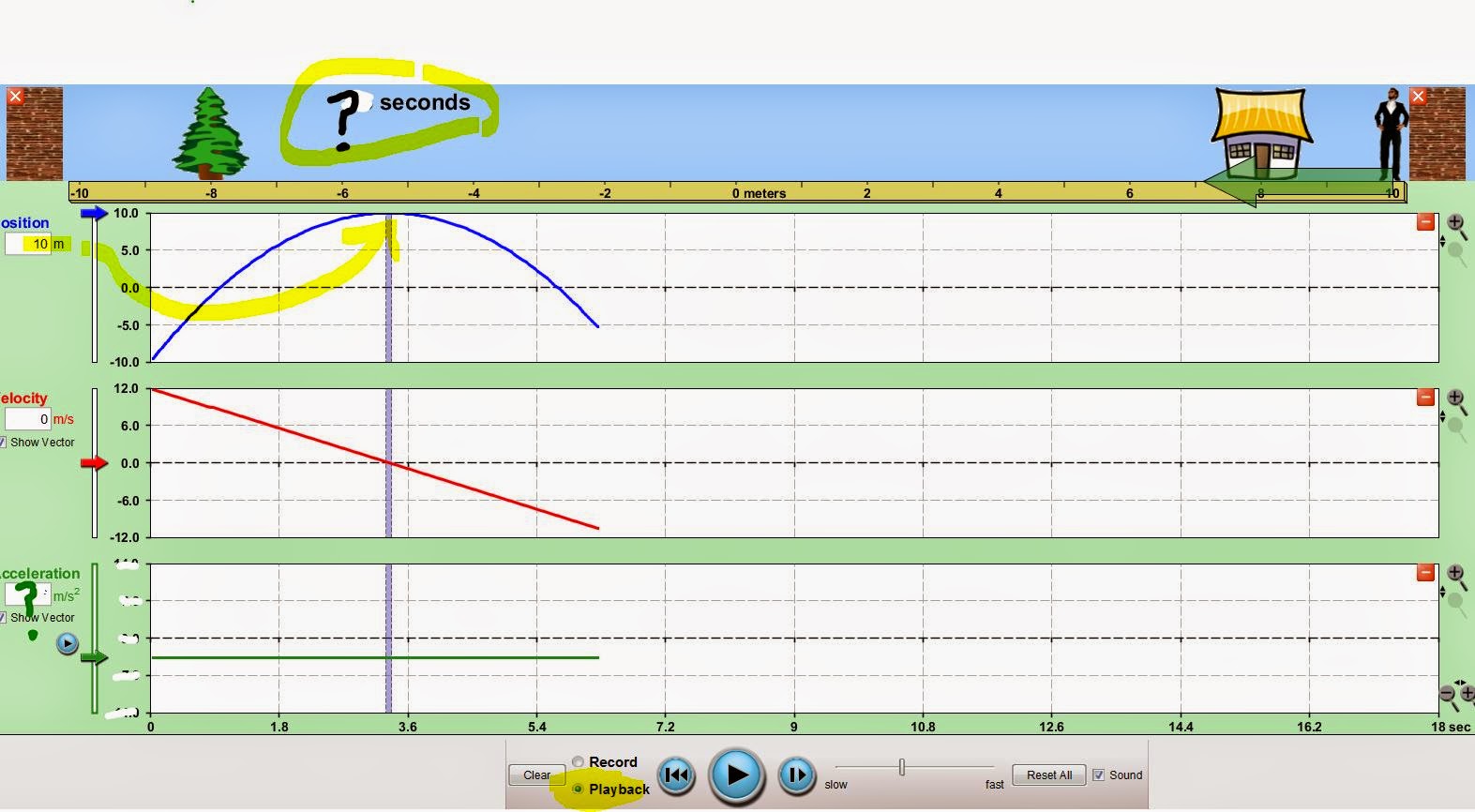
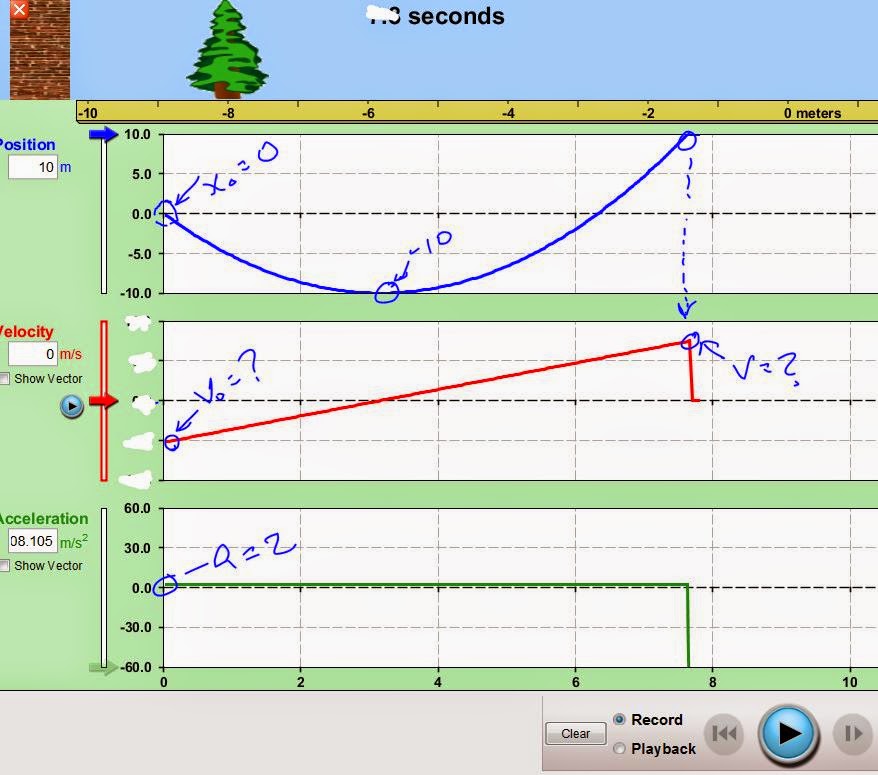
1. Start the running man at a position of -10 meters with a positive velocity of 12 m/s. Solve for what constant acceleration will bring the running man to a stop at 10m. How long does it take for the running man to reach the other wall? Show the equations you used to solve for acceleration.

Given:                                    Find:
xo = -10 m
x(tb) = +10 m                         a = constant = ___________
V0 = +12m/s
V(tb) = 0                                 tb = __________   (time to reach second wall)

Note: Use the playback feature to see the time (top of screen)! Grab the blue slider, and use the magnifying glass to zoom in on your graph.

2. This time, the running man start at x = 0, and has a constant acceleration of 2 m/s^2. What does his initial velocity need to be if he first runs to the -10m wall, turns around, and then runs all the way to the + 10 m wall? What is his velocity just before he crashes into the +10m wall? Show all of your calculations, and use the simulation to check your work!

3. The walking man starts out with a velocity of -6 m/s, and has a constant acceleration of 3 m/s^2. The starting position is such that he turns around at -10 m. What is his starting position? and what time does he reach x = +10? Show calculations!

4. Create your own constant acceleration problem! What is the minimum amount of information needed to solve it?

5. Under constant deceleration, if you double the initial walking speed, the amount of time it takes to stop
a) is two times longer
b) is four times longer
c) is half as long
d) is 1/4 as long

6. If the speed is increasing, the acceleration must be positive.
a) True
b) False

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Use the Expressions evaluator:
Special Features →Enter an expression for the position x as a function of time.

7. Create the same graphs from question #1 by entering an equation for x(t) in the expression evaluator. (Equation should start the running man at a position of -10 meters, with an initial velocity of 12 m/s, and an acceleration that bring him to a stop at 10m). See "help" to see how to enter equations.

write your equation for x(t) =

8. Write an equation for x(t) that produces a linearly increasing acceleration.

9. Write an equation for x(t) that produces a linearly decreasing acceleration. (Note. in some cases the simulation did not handle these equations very well - sorry! you can still calculate it though)

Pages

11.7-11.8