Use the velocity and radius of a weight swinging in a circle to measure acceleration due to gravity.
Please be considerate of those around you while swinging your weight!
Use a tennis
ball on the end of a string to measure gravitational acceleration.
Procedure:
1. Spin the tennis ball with a nice, steady, velocity.
2. Measure the radius or the rotation (distance
between the ball and the pole)
3.
Time how long it takes for one revolution (or time how long it takes for
10 revolutions, then divide to find the average time for one revolution). Use this time, and the radius/circumference
of the rotation to calculate velocity.
4. Measure the length of the string (L), and find the relationship between theta, v, L, and r.
5. Pretend that you do not know what “g” is, and
calculate it from the velocity of the ball, and theta.
Write an
equation for g as a function of v, r, and  . Do you need to know the mass of the ball to
solve for g?
. Do you need to know the mass of the ball to
solve for g?
Repeat
the same experiment 3 different times with 3 different velocities and
radius. Calculate g from each scenario,
and find the average value of g.
Why can
you never swing the weight fast enough to have a perfectly horizontal
string ?
Exercise #2:
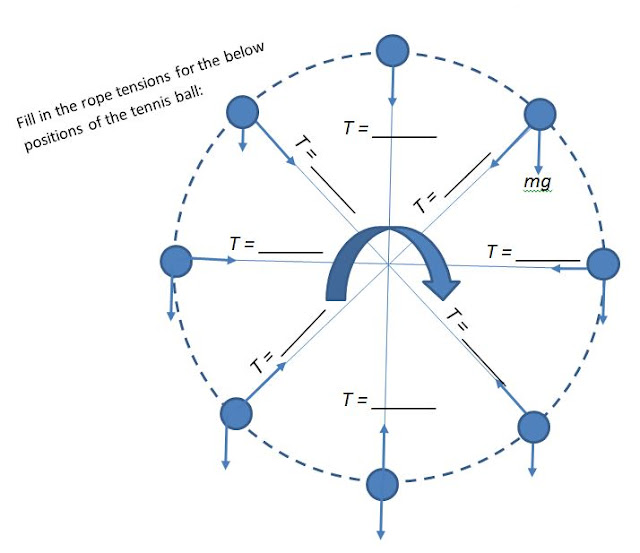
Swing the ball
vertically. When is the tension in the rope the greatest? When is it the
least? What velocity is required in order to keep the rope from going
slack? Measure the
length of the rope, weigh your tennis ball, calculate the needed velocity/RPM to keep the string from going slack, then test your calculations.
Try videotaping the slowest velocity you can swing the ball with while
keeping the rope taunt, and then getting the RPM’s off of your video-tape. Again, you can get better #’s if you time
5-10 rotations instead of just one.
The ice-bucket
challenge:
Extra credit if you make a good youtube of yourself swinging
a bucket of ice-water over your head! Calculate what RPM you need to keep all of the water in the bucket.
Youtube:
Ball on a String with Circular Motion: physics challenge problem
Tennis Ball Toss: Projectile Motion
Is motion in
the y direction really independent of motion in the x direction?
If you
finish everything, start the projectile motion simulation HW problems! (See HW in D2L)
Extra Credit:
Looking down on the weight's trajectory, consider the case where the velocity of the weight linearly increases with time. Use excel or mathematica to:
a) Graph the path of the rock in excel. Play around with different accelerations, and see what kinds of spirals you can create!
hint:
- Start with a column in excel for radius - vary the radius between 0 and almost the length of your string.
r
0
.01
.02
.03
.
.
.
L
next, calculate what velocity is needed to produce a given radius. Find the time that it takes for the tennis ball to reach your calculated velocity using tangential acceleration (it's easier to calculate t(r) than to find r(t)).
r t
0 0
.01 t1
.02 t2
.03 t3
. .
.
.
L
for linearly increasing velocity, v = 0 + at. Choose a constant acceleration, create new column with the velocity at each given time, and then find t(r).
r t v(t) = at
0 0 0
.01 t1 v(t1)
.02 t2 v(t2)
.03 t3 .
. .
.
.
L
Add a column for theta from the x axis, and then find (x,y_ = (LCos(theta), L Sin(theta))
You might have to play around with different dr's, L's and a's before you get a nice spiral! Check your units along the way to make sure you are on the right track. Your r's should never go beyond the length of your string - the needed velocity for radius approaching L should go to infinity (why the tennis ball cannot ever go horizontal etc.)
b) Graph normal, tangential, and total acceleration as a function of time for the system above. How does the normal acceleration compare with the tangential acceleration? Again, you can choose your own numbers for this, just choose something that shows the trends nicely.